Unión de sucesos
Dados dos sucesos, A y B, se llama suceso unión de A y B al suceso, A U B , que resulta si se obtiene el suceso A o el suceso B (o ambos), es decir, es el suceso formado por todos los resultados de A y de B juntos.
Probabilidad. Las leyes del azar
Operaciones con sucesos
Intersección de sucesos
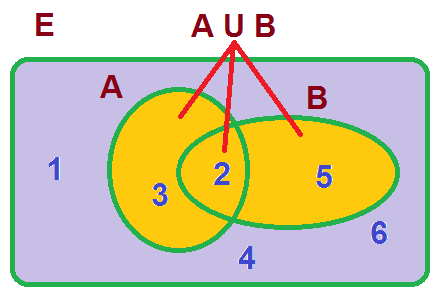
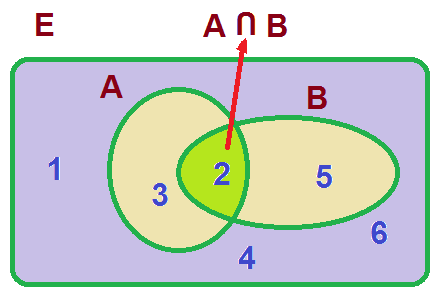
Dados dos sucesos, A y B, se denomina suceso intersección de A y B al suceso, A ∩ B, que resulta si se obtiene a la vez el suceso A y el suceso B, es decir, es el suceso formado por todos los resultados comunes de A y de B.
Complementario de un suceso
Dado el suceso A, se llama suceso contrario o complementario de A al suceso, Ac , que resulta si no se obtiene A, es decir, es el suceso formado por todos los resultados del experimento que no están en A.
Leyes de Morgan
Las Leyes de De Morgan consisten en dos propiedades que relacionan la unión, la intersección y el complementario:
\overline{A \cup B} = \overline{A} \cap \overline{B}
\overline{A \cap B} = \overline{A} \cup \overline{B}
Sucesos compatibles
Dos sucesos, A y B, son compatibles sin pueden obtenerse simultáneamente e incompatibles en caso contrario, es decir, si no pueden obtenerse a la vez. Por tanto:
- Si A ∩ B ≠ Ø entonces A y B son compatibles.
- Si A ∩ B = Ø entonces A y B son incompatibles.
Sucesos compatibles
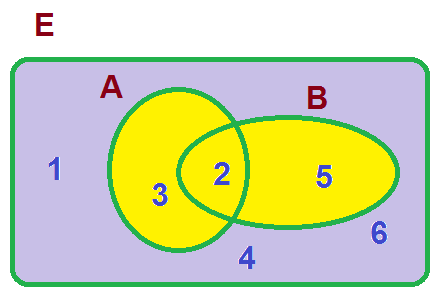
Sucesos incompatibles
Tarea multinivel
Nivel Básico
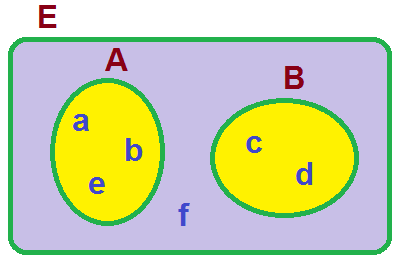
En un sorteo de lotería observamos la cifra en que termina el “gordo”.
a) ¿Cuál es el espacio muestral?
b)Escribe los sucesos:
- A = "menor que 5"
- B = "número par".
c) Halla los sucesos A ∪ B, A ∩ B, Ac, Bc, Ac ∩ Bc.
Nivel Intermedio
En el experimento que consiste en lanzar 3 veces una moneda, consideramos los siguientes sucesos.
- A=”sacar dos cruces”
- B=”salir alguna cara”
- C=”la última es una cruz”
a) Determina el espacio muestral con la ayuda de un diagrama de árbol.
b) Determina los siguientes sucesos:
- A ∩ C
- B ∪ C
- A ∩ B ∩ C
- A ∩ Bc
Nivel Avanzado
Se considera el experimento aleatorio lanzar un dado de seis caras y los sucesos:
A="obtener un número impar" y B="obtener un múltiplo de 3"
a) Establece el espacio muestral del experimento.
b) Indica si los sucesos A y B son elementales o compuestos.
c) Clasifica los sucesos A y B como compatibles o incompatibles.
d) Demuestra las leyes de Morgan a partir de los sucesos A y B.
Nivel Básico
En un sorteo de lotería observamos la cifra en que termina el “gordo”.
a) ¿Cuál es el espacio muestral?
E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
b)Escribe los sucesos:
- A = {0, 1, 2, 3, 4}
- B = {0, 2, 4, 6, 8}
c) Halla los sucesos A ∪ B, A ∩ B, Ac, Bc, Ac ∩ Bc.
A ∪ B = {0, 1, 2, 3, 4, 6, 8}
A ∩ B = {0, 2, 4}
Ac= {5, 6, 7, 8, 9}
Bc = {1, 3, 5, 7, 9}
Ac ∩ Bc = {5, 7, 9}
Nivel Intermedio
En el experimento que consiste en lanzar 3 veces una moneda, consideramos los siguientes sucesos.
A=”sacar dos cruces” = {CXX,XCX,XXC}
B=”salir alguna cara” = {CCC, CCX, CXC, CXX, XCC, XCX, XXC}
C=”la última es una cruz” = {CCX, CXX, XCX, XXX}
a) Determina el espacio muestral con la ayuda de un diagrama de árbol.
E= { CCC, CCX, CXC, CXX, XCC, XCX, XXC, XXX }
b) Determina los siguientes sucesos:
- A ∩ C = {CXX, XCX}
- B ∪ C = E
- A ∩ B ∩ C = {CXX, XCX}
- A ∩ Bc = Ø (conjunto vacío)
Nivel Avanzado
Se considera el experimento aleatorio lanzar un dado de seis caras y los sucesos:
A="obtener un número impar"={1, 3, 5}
B="obtener un múltiplo de 3"={3, 6}
a) Establece el espacio muestral del experimento.
E={1, 2, 3, 4, 5, 6}
b) Indica si los sucesos A y B son elementales o compuestos.
Los sucesos A y B son compuestos ya que tienen más de un elemento.
c) Clasifica los sucesos A y B como compatibles o incompatibles.
Los sucesos son compatibles ya que tienen un elemento en común: A ∩ B = {3}
d) Demuestra las leyes de Morgan a partir de los sucesos A y B.
Tenemos que
A ∪ B = {1, 3, 5, 6} y (A ∪ B)c = {2, 4}
Ac = {2, 4, 6}, Bc = {1, 2, 4 y 5} por tanto Ac ∩ Bc = {2, 4} y Ac ∪ Bc = {1, 2, 4, 5, 6}
Además A ∩ B = {3}, por tanto (A ∩ B)c = {1, 2, 4, 5, 6}
Por tanto se cumplen las dos leyes de Morgan:
- (A ∪ B)c = Ac ∩ Bc = {2, 4}
- (A ∩ B)c = Ac ∪ Bc = {1, 2, 4, 5, 6}
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0